FISIKA
DASAR
Mata kuliah ini merupakan prasyarat
bagi kelompok mata kuliah keahlian program studi pada program S-1 Program Studi
Teknologi Informasi dan Komunikasi. Setelah mengikuti perkuliahan ini mahasiswa
diharapkan mampu menguasai pengetahuan dasar mekanika, gelombang, bunyi, optika
dan panas serta dapat mengembangkan dan mengaplikasikannya untuk mempelajari
pengetahuan fisika yang lebih tinggi. Dalam perkuliahan ini dibahas gerak satu
dimensi, gerak dua dimensi, dinamika, usaha dan energi, momentum linear dan
tumbukan, rotasi, keseimbangan, gravitasi, mekanika fluida, getaran, gelombang
bunyi, optika dan panas. Perkuliahan dilaksanakan menggunakan pendekatan
konseptual dan kontekstual dengan metoda demonstrasi, diskusi, tanya jawab, dan
ceramah, dilengkapi dengan penggunaan OHP, dan alat peraga fisika.
Adapun Materi untuk Perkuliahan
dapat diunduh pada link di bawah ini:
1. Besaran Dan Satuan
Pengukuran adalah proses membandingkan nilai besaran
yang diukur dengan besaran sejenis yang dipakai sebagai satuan. Hasil
dari pada pengukuran merupakan besaran. Besaran adalah suatu yang dapat diukur dan dinyatakan dengan angka dan nilai yang memiliki satuan.
Dari pengertian ini dapat diartikan bahwa sesuatu itu dapat dikatakan sebagai besaran harus mempunyai 3 syarat yaitu
1. dapat diukur atau dihitung
2. dapat dinyatakan dengan angka-angka atau mempunyai nilai
3. mempunyai satuan
Bila ada satu saja dari syarat tersebut diatas tidak dipenuhi maka sesuatu itu tidak dapat dikatakan sebagai besaran.
Besaran berdasarkan cara memperolehnya dapat dikelompokkan menjadi 2 macam yaitu :
1. Besaran Fisika yaitu besaran yang diperoleh dari pengukuran. Karena diperoleh dari pengukuran maka harus ada alat ukurnya. Sebagai contoh adalah massa. Massa merupakan besaran fisika karena massa dapat diukur dengan menggunakan neraca.
2. Besaran non Fisika yaitu besaran yang diperoleh dari penghitungan. Dalam hal ini tidak diperlukan alat ukur tetapi alat hitung sebagai misal kalkulator. Contoh besaran non fisika adalah Jumlah.
Dalam fisika besaran ada dua yaitu besaran pokok dan besaran turunan.
Besaran pokok adalah besaran yang satuannya telah ditetapkan terlebih dahulu dan tidak diturunkan dari besaran lain.
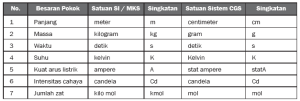
Besaran pokok yang paling umum ada 7 macam yaitu Panjang (m), Massa (kg), Waktu (s), Suhu (K), Kuat Arus Listrik (A), Intensitas Cahaya (cd), dan Jumlah Zat (mol). Besaran pokok mempunyai ciri khusus antara lain diperoleh dari pengukuran langsung, mempunyai satu satuan (tidak satuan ganda), dan ditetapkan terlebih dahulu.
Besaran turunan adalah besaran yang satuannya diturunkan dari besaran pokok. Jika suatu besaran turunan merupakan perkalian besaran pokok , satuan besaran turunan itu juga merupakan perkalian satuan besaran pokok, begitu juga berlaku didalam satuan besaran turunan yang merupakan pembagian besaran pokok. Besaran turunan mempunyai ciri khusus antara lain : diperoleh dari pengukuran langsung dan tidak langsung, mempunyai satuan lebih dari satu dan diturunkan dari besaran pokok.
Satuan adalah sebagai pembanding dalam suatu pengukuran besaran. Setiap besaran mempunyai satuan masing-masing, tidak mungkin dalam 2 besaran yang berbeda mempunyai satuan yang sama. Apa bila ada dua besaran berbeda kemudian mempunyai satuan sama maka besaran itu pada hakekatnya adalah sama. Sebagai contoh Gaya (F) mempunyai satuan Newton dan Berat (w) mempunyai satuan Newton. Besaran ini kelihatannya berbeda tetapi sesungguhnya besaran ini sama yaitu besaran turunan gaya.
a. Satuan Baku
Satuan baku adalah satuan yang telah diakui dan disepakati pemakaiannya secara internasional tau disebut dengan satuan internasional (SI).
Contoh: meter, kilogram, dan detik.
Sistem satuan internasional dibagi menjadi dua, yaitu:
1. Sistem MKS (Meter Kilogram Sekon)
2. Sistem CGS (Centimeter Gram Second)
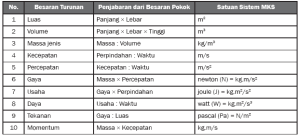
Tabel Satuan Baku
b. Satuan Tidak Baku
Satuan tidak baku adalah satuan yang tidak diakui secara internasional dan hanya digunakan pada suatu wilayah tertentu.
Contoh: depa, hasta, kaki, lengan, tumbak, bata dan langkah.
ALAT UKUR
Alat Ukur adalah sesuatu yang digunakan untuk mengukur suatu besaran.
Berbagai macam alat ukur memiliki tingkat ketelitian tertentu. Hal ini bergantung pada skala terkecil alat ukur tersebut. Semakin kecil skala yang tertera pada alat ukur maka semakin tinggi ketelitian alat ukur tersebut. Beberapa contoh alat ukur sesuai dengan besarannya, yaitu:
a. Alat Ukur Panjang
1. Mistar (Penggaris)
Mistar adalah ala ukur panjang dengan ketelitian sampai 0,1 cm atau 1 mm. Pada pembacaan skala, kedudukan mata pengamat harus tegak lurus dengan skala mistar yang di baca.
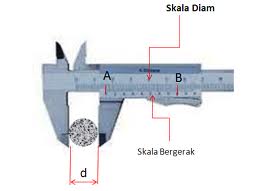
2. Jangka Sorong
Jangka sorong dipakai untuk mengukur suatu benda dengan panjang yang kurang dari 1mm. Skala terkecil atau tingkat ketelitian pengukurannya sampai dengan 0,01 cm atau 0,1 mm.
Umumnya, jangka sorong digunakan untuk mengukur panjang suatu benda, diameter bola, ebal uang logam, dan diameter bagian dalam tabung.
Jangka sorong memiliki dua skala pembacaan, yaitu:
a). Skala Utama/tetap, yang terdapat pada rahang tetap jangka sorong.
b). Skala Nonius, yaitu skala yang terdapat pada rahang sorong yang dapa bergeser/digerakan.
3. Mikrometer Sekrup
Mikrometer sekrup merupakan alat ukur panjang dengan ingkat ketelitian terkecil yaiu 0,01 mm atau 0,001 cm.
Skala terkecil (skala nonius) pada mikrometer sekrup terdapat pada rahang geser, sedangkan skala utama terdapat pada rahang tetap.
Mikrometer sekrup digunakan untuk mengukur diameter benda bundar dan plat yang sangat tipis.
b. Alat Ukur Massa
Alat ukur yang digunakan untuk mengukur massa suatu benda adalah neraca. Berdasarkan cara kerjanya dan keelitiannya neraca dibedakan menjadi tiga, yaitu:
1. Neraca digital, yaitu neraca yang bekerja dengan sistem elektronik. Tingkat ketelitiannya hingga 0,001g.
2. Neraca O’Hauss, yaitu neraca dengan tingkat ketelitian hingga 0.01 g.
3. Neraca sama lengan, yaitu neraca dengan tingkat ketelitian mencapai 1 mg atau 0,001 g.
c. Alat Ukur Waktu
Satuan internasional untuk waktu adalah detik atau sekon. Satu sekon standar adalah waktu yang dibuuhkan oleh atom Cesium-133 untuk bergetar sebanyak 9.192.631.770 kali.
Alat yang digunakan untuk mengukur waktu, antara lain jam matahari, jam dinding, arloji (dengan ketelitian 1 sekon), dan stopwatch (ketelitian 0,1 sekon).
Besaran berdasarkan arah dapat dibedakan menjadi 2 macam
Angka Penting : Semua angka yang diperoleh dari hasil pengukuran dengan alat ukur, terdiri dari :
• Angka pasti
• Angka taksiran
Aturan :
a. Penjumlahan / Pengurangan
Ditulis berdasarkan desimal paling sedikit
Contoh :
2,7481
8,41
——- +
11,1581 ——> 11,16
b. Perkalian / Pembagian
Ditulis berdasarkan angka penting paling sedikit
Contoh :
4,756
110
———
0000
4756
4756
————– +
523,160 —-> 520
Dari pengertian ini dapat diartikan bahwa sesuatu itu dapat dikatakan sebagai besaran harus mempunyai 3 syarat yaitu
1. dapat diukur atau dihitung
2. dapat dinyatakan dengan angka-angka atau mempunyai nilai
3. mempunyai satuan
Bila ada satu saja dari syarat tersebut diatas tidak dipenuhi maka sesuatu itu tidak dapat dikatakan sebagai besaran.
Besaran berdasarkan cara memperolehnya dapat dikelompokkan menjadi 2 macam yaitu :
1. Besaran Fisika yaitu besaran yang diperoleh dari pengukuran. Karena diperoleh dari pengukuran maka harus ada alat ukurnya. Sebagai contoh adalah massa. Massa merupakan besaran fisika karena massa dapat diukur dengan menggunakan neraca.
2. Besaran non Fisika yaitu besaran yang diperoleh dari penghitungan. Dalam hal ini tidak diperlukan alat ukur tetapi alat hitung sebagai misal kalkulator. Contoh besaran non fisika adalah Jumlah.
Dalam fisika besaran ada dua yaitu besaran pokok dan besaran turunan.
Besaran pokok adalah besaran yang satuannya telah ditetapkan terlebih dahulu dan tidak diturunkan dari besaran lain.
Besaran pokok yang paling umum ada 7 macam yaitu Panjang (m), Massa (kg), Waktu (s), Suhu (K), Kuat Arus Listrik (A), Intensitas Cahaya (cd), dan Jumlah Zat (mol). Besaran pokok mempunyai ciri khusus antara lain diperoleh dari pengukuran langsung, mempunyai satu satuan (tidak satuan ganda), dan ditetapkan terlebih dahulu.
Besaran turunan adalah besaran yang satuannya diturunkan dari besaran pokok. Jika suatu besaran turunan merupakan perkalian besaran pokok , satuan besaran turunan itu juga merupakan perkalian satuan besaran pokok, begitu juga berlaku didalam satuan besaran turunan yang merupakan pembagian besaran pokok. Besaran turunan mempunyai ciri khusus antara lain : diperoleh dari pengukuran langsung dan tidak langsung, mempunyai satuan lebih dari satu dan diturunkan dari besaran pokok.
Satuan adalah sebagai pembanding dalam suatu pengukuran besaran. Setiap besaran mempunyai satuan masing-masing, tidak mungkin dalam 2 besaran yang berbeda mempunyai satuan yang sama. Apa bila ada dua besaran berbeda kemudian mempunyai satuan sama maka besaran itu pada hakekatnya adalah sama. Sebagai contoh Gaya (F) mempunyai satuan Newton dan Berat (w) mempunyai satuan Newton. Besaran ini kelihatannya berbeda tetapi sesungguhnya besaran ini sama yaitu besaran turunan gaya.
a. Satuan Baku
Satuan baku adalah satuan yang telah diakui dan disepakati pemakaiannya secara internasional tau disebut dengan satuan internasional (SI).
Contoh: meter, kilogram, dan detik.
Sistem satuan internasional dibagi menjadi dua, yaitu:
1. Sistem MKS (Meter Kilogram Sekon)
2. Sistem CGS (Centimeter Gram Second)
Tabel Satuan Baku
Besaran Pokok
|
Satuan MKS
|
Satuan CGS
|
Massa
|
kilogram (kg)
|
gram (g)
|
Panjang
|
meter (m)
|
centimeter (cm)
|
Waktu
|
sekon (s)
|
sekon (s)
|
Kuat Arus
|
ampere (A)
|
statampere (statA)
|
Suhu
|
kelvin (K)
|
kelvin (K)
|
Intensitas Cahaya
|
candela (Cd)
|
candela (Cd)
|
Jumlah Zat
|
kilomole (mol)
|
mol
|
Satuan tidak baku adalah satuan yang tidak diakui secara internasional dan hanya digunakan pada suatu wilayah tertentu.
Contoh: depa, hasta, kaki, lengan, tumbak, bata dan langkah.
ALAT UKUR
Alat Ukur adalah sesuatu yang digunakan untuk mengukur suatu besaran.
Berbagai macam alat ukur memiliki tingkat ketelitian tertentu. Hal ini bergantung pada skala terkecil alat ukur tersebut. Semakin kecil skala yang tertera pada alat ukur maka semakin tinggi ketelitian alat ukur tersebut. Beberapa contoh alat ukur sesuai dengan besarannya, yaitu:
a. Alat Ukur Panjang
1. Mistar (Penggaris)
Mistar adalah ala ukur panjang dengan ketelitian sampai 0,1 cm atau 1 mm. Pada pembacaan skala, kedudukan mata pengamat harus tegak lurus dengan skala mistar yang di baca.
2. Jangka Sorong
Jangka sorong dipakai untuk mengukur suatu benda dengan panjang yang kurang dari 1mm. Skala terkecil atau tingkat ketelitian pengukurannya sampai dengan 0,01 cm atau 0,1 mm.
Umumnya, jangka sorong digunakan untuk mengukur panjang suatu benda, diameter bola, ebal uang logam, dan diameter bagian dalam tabung.
Jangka sorong memiliki dua skala pembacaan, yaitu:
a). Skala Utama/tetap, yang terdapat pada rahang tetap jangka sorong.
b). Skala Nonius, yaitu skala yang terdapat pada rahang sorong yang dapa bergeser/digerakan.
3. Mikrometer Sekrup
Mikrometer sekrup merupakan alat ukur panjang dengan ingkat ketelitian terkecil yaiu 0,01 mm atau 0,001 cm.
Skala terkecil (skala nonius) pada mikrometer sekrup terdapat pada rahang geser, sedangkan skala utama terdapat pada rahang tetap.
Mikrometer sekrup digunakan untuk mengukur diameter benda bundar dan plat yang sangat tipis.
b. Alat Ukur Massa
Alat ukur yang digunakan untuk mengukur massa suatu benda adalah neraca. Berdasarkan cara kerjanya dan keelitiannya neraca dibedakan menjadi tiga, yaitu:
1. Neraca digital, yaitu neraca yang bekerja dengan sistem elektronik. Tingkat ketelitiannya hingga 0,001g.
2. Neraca O’Hauss, yaitu neraca dengan tingkat ketelitian hingga 0.01 g.
3. Neraca sama lengan, yaitu neraca dengan tingkat ketelitian mencapai 1 mg atau 0,001 g.
c. Alat Ukur Waktu
Satuan internasional untuk waktu adalah detik atau sekon. Satu sekon standar adalah waktu yang dibuuhkan oleh atom Cesium-133 untuk bergetar sebanyak 9.192.631.770 kali.
Alat yang digunakan untuk mengukur waktu, antara lain jam matahari, jam dinding, arloji (dengan ketelitian 1 sekon), dan stopwatch (ketelitian 0,1 sekon).
Besaran berdasarkan arah dapat dibedakan menjadi 2 macam
- Besaran vektor adalah besaran yang mempunyai nilai dan arah sebagai contoh besaran kecepatan, percepatan dan lain-lain.
- Besaran sekalar adalah besaranyang mempunyai nilai saja sebagai contoh kelajuan, perlajuan dan lain-lain.
Angka Penting : Semua angka yang diperoleh dari hasil pengukuran dengan alat ukur, terdiri dari :
• Angka pasti
• Angka taksiran
Aturan :
a. Penjumlahan / Pengurangan
Ditulis berdasarkan desimal paling sedikit
Contoh :
2,7481
8,41
——- +
11,1581 ——> 11,16
b. Perkalian / Pembagian
Ditulis berdasarkan angka penting paling sedikit
Contoh :
4,756
110
———
0000
4756
4756
————– +
523,160 —-> 520
2. Vektor
Vektor adalah jenis besaran yang mempunyai nilai dan arah. Besaran yang termasuk besaran vektor antara lain perpindahan, gaya, kecepatan, percepatan, dan lain lain. Sebuah vektor digambarkan sebagai sebuah ruas garis berarah yang mempunyai titik tangkap (titik pangkal) sebagai tempat permulaan vektor itu bekerja. Panjang garis menunjukkan nilai vektor dan arah panah menunjukkan arah vektor itu bekerja. Garis yang melalui vektor tersebut dinamakan garis kerja.
Penulisan sebuah simbol besaran vektor dengan menggunakan huruf tegak dicetak tebal, misalnya vektor AB ditulis AB. Selain itu, dapat pula dinyatakan dengan huruf miring dengan tanda panah di atasnya :
Besar (nilai) sebuah vektor
dinyatakan dengan huruf miring AB. Selain itu dapat pula dituliskan
dalam garis mutlak, yaitu dua garis tegak sejajar, pada kedua sisi
notasi vektor, misalnya, besarnya vektor AB = AB = |AB|.
Menggambar Vektor Dalam Bidang Datar (Dua Sumbu)
Pada bidang datar, vektor mempunyai dua komponen yaitu pada sumbu x dan sumbu y,
tampak seperti pada gambar diatas. Sebuah vektor dapat saja mempunyai
satu komponen bila vektor tersebut berada pada salah satu sumbu x atau y. Komponen vektor
adalah vektor-vektor yang bekerja pada saat yang bersamaan sehingga
menghasilkan satu vektor dengan arah tertentu (resultan). Oleh karena
vektor tergantung pada besar dan arah, maka vektor tersebut dapat
dipindahkan titik tangkapnya asal besar dan arahnya tetap.
Penulisan matematis A dapat ditulis dalam komponenkomponennya : A = Ax + A y; A merupakan jumlah dari komponen-komponennya.
Cara lain untuk menuliskan vektor, yaitu:
A = Axi + A y j
Dimana Ax dan Ay menunjukan besar (harga) vektor pada masing-masing komponen sumbu x dan sumbu y, sedangkan i dan j adalah vektor satuan pada masing-masing komponen sumbu x dan sumbu y.
Vektor Satuan
Vektor satuan adalah vektor yang besar/harganya satu satuan; vektor yang telah diuraikan ke sumbu x(i), sumbu y(j), dan sumbu z(k). Dikatakan vektor satuan karena besar vektor = |i| = |j| = |k| = 1. Misalnya, vektor A mempunyai komponen sumbu x(Ax ), pada sumbu y(Ay ) dan sumbu z(Az ), maka vektor A dapat ditulis dalam lambang vektor sebagai berikut.
A = Ax i + Ax j + Ax k
Panjang vektor A adalah :
3. KINEMATIKA
1. Gerak Lurus Beraturan (GLB)
KINEMATIKA adalah Ilmu gerak yang membicarakan gerak suatu benda tanpa memandang gaya yang bekerja pada benda tersebut (massa benda diabaikan). Jadi jarak yang ditempuh benda selama geraknya hanya ditentukan oleh kecepatan v dan atau percepatan a.
Gerak Lurus Beraturan (GLB) adalah gerak lurus pada arah mendatar dengan kocepatan v tetap (percepatan a = 0), sehingga jarakyang ditempuh S hanya ditentukan oleh kecepatan yang tetap dalam waktu tertentu.
Pada umumaya GLB didasari oleh Hukum Newton I ( S F = 0 ).
Tanda D (selisih) menyatakan nilai rata-rata.
Tanda d (diferensial) menyatakan nilai sesaat.
2. Gerak Lurus Berubah Beraturan (GLBB)
Gerak Lurus Berubah Beraturan (GLBB) adalah gerak lurus pada arah mendatar dengan kecepatan v yang berubah setiap saat karena adanya percepatan yang tetap. Dengan kata lain benda yang melakukan gerak dari keadaan diam atau mulai dengan kecepatan awal akan berubah kecepatannya karena ada percepatan (a= +) atau perlambatan (a= -).
Pada umumnya GLBB didasari oleh Hukum Newton II ( S F = m . a ).
vt = kecepatan sesaat benda
v0 = kecepatan awal benda
S = jarak yang ditempuh benda
f(t) = fungsi dari waktu t
Syarat : Jika dua benda bergerak dan saling bertemu maka jarak yang ditempuh kedua benda adalah sama.
3. Grafik Gerak Benda
Grafik gerak benda (GLB dan GLBB) pada umumnya terbagi dua, yaitu S-t dan grafik v-t.
Pemahaman grafik ini penting untuk memudahkan penyelesaian soal.
Khusus untuk grafik v-t maka jarak yang ditempuh benda dapat dihitung dengan cara menghitung luas dibawah kurva grafik tersebut.
4. Gerak Karena pengaruh Gravitasi
g = percepatan gravitasi bumi.
y = h = lintasan yang ditempuh benda pada arah vertikal,(diukur dari posisi benda mula-mula).
t = waktu yang dibutuhkan benda untuk menempuh lintasannya.
syarat suatu benda mencapai tinggi maksimum (h maks): Vt = 0
Dalam penyelesaian soal gerak vertikal keatas, lebih mudah diselesaikan dengan menganggap posisi di tanah adalah untuk Y = 0.
Contoh:
1. Sebuah partikel bergerak sepanjang sumbu-X dengan persamaan lintasannya: X = 5t2 + 1, dengan X dalam meter dan t dalam detik. Tentukan:
a. Kecepatan rata-rata antara t = 2 detik dan t = 3 detik.
b. Kecepatan pada saat t = 2 detik.
c. Jarak yang ditempah dalam 10 detik.
d. Percepatan rata-rata antara t = 2 detik dan t = 3 detik.
Jawab:
a. v rata-rata = DX / Dt = (X3 - X2) / (t3 - t2) = [(5 . 9 + 1) - (5 . 4 + 1)] / [3 - 2] = 46 - 21 = 25 m/ detik
b. v2 = dx/dt |t=2 = 10 |t=2 = 20 m/detik.
c. X10 = ( 5 . 100 + 1 ) = 501 m ; X0 = 1 m
Jarak yang ditempuh dalam 10 detik = X10 - X0 = 501 - 1 = 500 m
d. a rata-rata = Dv / Dt = (v3- v2)/(t3 - t2) = (10 . 3 - 10 . 2)/(3 - 2) = 10 m/det2
2. Jarak PQ = 144 m. Benda B bergerak dari titik Q ke P dengan percepatan 2 m/s2 dan kecepatan awal 10 m/s. Benda A bergerak 2 detik kemudian dari titik P ke Q dengan percepatan 6 m/s2 tanpa kecepatan awal. Benda A dan B akan bertemu pada jarak berapa ?
Jawab:
Karena benda A bergerak 2 detik kemudian setelah benda B maka tB = tA + 2.
 SA = v0.tA + 1/2 a.tA2 = 0 + 3 tA2
SA = v0.tA + 1/2 a.tA2 = 0 + 3 tA2
SB = v0.tB + 1/2 a.tB2 = 10 (tA + 2) + (tA + 2)2
Misalkan kedua benda bertemu di titik R maka
SA + SB = PQ = 144 m
3tA2 + 10 (tA + 2) + (tA + 2)2 = 144
2tA2 + 7tA - 60 = 0
Jadi kedua benda akan bertemu pada jarak SA = 3tA2 = 48 m (dari titik P).
3. Grafik di bawah menghubungkan kocepatan V dan waktu t dari dua mobil A dan B, pada lintasan dan arah sama. Jika tg a = 0.5 m/det, hitunglah:
a. Waktu yang dibutuhkan pada saat kecepatan kedua mobil sama.
b. Jarak yang ditempuh pada waktu menyusul
Jawab:
 Dari grafik terlihat jenis gerak benda A dan B adalah GLBB dengan V0(A) = 30 m/det dan V0(B) = 0.
Dari grafik terlihat jenis gerak benda A dan B adalah GLBB dengan V0(A) = 30 m/det dan V0(B) = 0.
a. Percepatan kedua benda dapat dihitung dari gradien garisnya,
jadi : aA = tg a = 0.5
10/t = 0.5 ® t = 20 det
aB = tg b = 40/20 = 2 m/det
b. Jarak yang ditempuh benda
SA = V0 t + 1/2 at2 = 30t + 1/4t2
SB = V0 t + 1/2 at2 = 0 + t2
pada saat menyusul/bertemu : SA = SB ® 30t + 1/4 t2 = t2 ® t = 40 det
Jadi jarak yang ditempuh pada saat menyusul : SA = SB = 1/2 . 2 . 402 = 1600 meter
5. Gerak Berbentuk Parabola
Gerak ini terdiri dari dua jenis, yaitu:
1. Gerak Setengah Parabola
Benda yang dilempar mendatar dari suatu ketinggian tertentu dianggap tersusun atas dua macam gerak, yaitu :
2. Gerak Parabola/Peluru
Benda yang dilempar ke atas dengan sudut tertentu, juga tersusun atas dua macam gerak dimana lintasan
dan kecepatan benda harus diuraikan pada arah X dan Y.
Syarat mencapai titik P (titik tertinggi): vy = 0
top = v0 sin q / g
sehingga
top = tpqtoq = 2 top
OQ = v0x tQ = V02 sin 2q / g
h max = v oy tp - 1/2 gtp2 = V02 sin2 q / 2g
vt = Ö (vx)2 + (vy)2
Contoh:
1. Sebuah benda dijatuhkan dari pesawat terbang yang sedang melaju horisontal 720 km/jam dari ketinggian 490 meter. Hitunglah jarak jatuhnya benda pada arah horisontal ! (g = 9.8 m/det2). Jawab:
2. Peluru A dan peluru B ditembakkan dari senapan yang sama dengan sudut elevasi yang berbeda; peluru A dengan 30o dan peluru B dengan sudut 60o. Berapakah perbandingan tinggi maksimum yang dicapai peluru A dan peluru B?
Jawab:
Peluru A:
hA = V02 sin2 30o / 2g = V02 1/4 /2g = V02 / 8g
Peluru B:
hB = V02 sin2 60o / 2g = V02 3/4 /2g = 3 V02 / 8g
hA = hB = V02/8g : 3 V02 / 8g = 1 : 3
6. Gerak Melingkar
Gerak melingkar terbagi dua, yaitu:
1. GERAK MELINGKAR BERATURAN (GMB)
GMB adalah gerak melingkar dengan kecepatan sudut (w) tetap.
2. GERAK MELINGKAR BERUBAH BERATURAN (GMBB)
GMBB adalah gerak melingkar dengan percepatan sudut a tetap.
Dalam gerak ini terdapat percepatan tangensial aT = percepatan linier, merupakan percepatan yang arahnya menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan v).
a = Dw/Dt = aT / R
aT = dv/dt = a R
T = perioda (detik)
R = jarijari lingkaran.
a = percepatan angular/sudut (rad/det2)
aT = percepatan tangensial (m/det2)
w = kecepatan angular/sudut (rad/det)
q = besar sudut (radian)
S = panjang busur
Hubungan besaran linier dengan besaran angular:
Contoh:
1. Sebuah mobil bergerak pada jalan yang melengkung dengan jari-jari 50 m. Persamaan gerak mobil untuk S dalam meter dan t dalam detik ialah:
S = 10+ 10t - 1/2 t2
Hitunglah:
Kecepatan mobil, percepatan sentripetal dan percepatan tangensial pada saat t = 5 detik !Jawab:
v = dS/dt = 10 - t; pada t = 5 detik, v5 = (10 - 5) = 5 m/det.
- percepatan sentripetal : aR = v52/R = 52/50 = 25/50 = 1/2 m/det2
- percepatan tangensial : aT = dv/dt = -1 m/det
KINEMATIKA adalah Ilmu gerak yang membicarakan gerak suatu benda tanpa memandang gaya yang bekerja pada benda tersebut (massa benda diabaikan). Jadi jarak yang ditempuh benda selama geraknya hanya ditentukan oleh kecepatan v dan atau percepatan a.
Gerak Lurus Beraturan (GLB) adalah gerak lurus pada arah mendatar dengan kocepatan v tetap (percepatan a = 0), sehingga jarakyang ditempuh S hanya ditentukan oleh kecepatan yang tetap dalam waktu tertentu.
Pada umumaya GLB didasari oleh Hukum Newton I ( S F = 0 ).
S = X = v . t ; a = Dv/Dt = dv/dt = 0
|
v = DS/Dt = ds/dt = tetap
|
Tanda D (selisih) menyatakan nilai rata-rata.
Tanda d (diferensial) menyatakan nilai sesaat.
2. Gerak Lurus Berubah Beraturan (GLBB)
Gerak Lurus Berubah Beraturan (GLBB) adalah gerak lurus pada arah mendatar dengan kecepatan v yang berubah setiap saat karena adanya percepatan yang tetap. Dengan kata lain benda yang melakukan gerak dari keadaan diam atau mulai dengan kecepatan awal akan berubah kecepatannya karena ada percepatan (a= +) atau perlambatan (a= -).
Pada umumnya GLBB didasari oleh Hukum Newton II ( S F = m . a ).
vt = v0 + a.t
vt2 = v02 + 2 a S
S = v0 t + 1/2 a t2
|
v0 = kecepatan awal benda
S = jarak yang ditempuh benda
f(t) = fungsi dari waktu t
v = ds/dt = f (t)
a = dv/dt = tetap
|
3. Grafik Gerak Benda
Grafik gerak benda (GLB dan GLBB) pada umumnya terbagi dua, yaitu S-t dan grafik v-t.
Pemahaman grafik ini penting untuk memudahkan penyelesaian soal.
Khusus untuk grafik v-t maka jarak yang ditempuh benda dapat dihitung dengan cara menghitung luas dibawah kurva grafik tersebut.
| GRAFIK GLB (v = tetap ; S - t) | GRAFIK GLBB (a = tetap ; v - t ; S - t2) |
| GERAK JATUH BEBAS: | adalah gerak jatuh benda pada arah vertikal dari ketinggian h tertentu tanpa kecepatan awal (v0 = 0), jadi gerak benda hanya dipengaruhi oleh gravitasi bumi g. |
y = h = 1/2 gt2t = Ö(2 h/g)
yt = g t = Ö(2 g h) |
y = h = lintasan yang ditempuh benda pada arah vertikal,(diukur dari posisi benda mula-mula).
t = waktu yang dibutuhkan benda untuk menempuh lintasannya.
| GERAK VERTIKAL KE ATAS: | adalah gerak benda yang dilempar dengan suatu kecepatan awal v0 pada arah vertikal, sehingga a = -g (melawan arah gravitasi). |
Dalam penyelesaian soal gerak vertikal keatas, lebih mudah diselesaikan dengan menganggap posisi di tanah adalah untuk Y = 0.
Contoh:
1. Sebuah partikel bergerak sepanjang sumbu-X dengan persamaan lintasannya: X = 5t2 + 1, dengan X dalam meter dan t dalam detik. Tentukan:
a. Kecepatan rata-rata antara t = 2 detik dan t = 3 detik.
b. Kecepatan pada saat t = 2 detik.
c. Jarak yang ditempah dalam 10 detik.
d. Percepatan rata-rata antara t = 2 detik dan t = 3 detik.
Jawab:
a. v rata-rata = DX / Dt = (X3 - X2) / (t3 - t2) = [(5 . 9 + 1) - (5 . 4 + 1)] / [3 - 2] = 46 - 21 = 25 m/ detik
b. v2 = dx/dt |t=2 = 10 |t=2 = 20 m/detik.
c. X10 = ( 5 . 100 + 1 ) = 501 m ; X0 = 1 m
Jarak yang ditempuh dalam 10 detik = X10 - X0 = 501 - 1 = 500 m
d. a rata-rata = Dv / Dt = (v3- v2)/(t3 - t2) = (10 . 3 - 10 . 2)/(3 - 2) = 10 m/det2
2. Jarak PQ = 144 m. Benda B bergerak dari titik Q ke P dengan percepatan 2 m/s2 dan kecepatan awal 10 m/s. Benda A bergerak 2 detik kemudian dari titik P ke Q dengan percepatan 6 m/s2 tanpa kecepatan awal. Benda A dan B akan bertemu pada jarak berapa ?
Jawab:
Karena benda A bergerak 2 detik kemudian setelah benda B maka tB = tA + 2.
SB = v0.tB + 1/2 a.tB2 = 10 (tA + 2) + (tA + 2)2
Misalkan kedua benda bertemu di titik R maka
SA + SB = PQ = 144 m
3tA2 + 10 (tA + 2) + (tA + 2)2 = 144
2tA2 + 7tA - 60 = 0
Jadi kedua benda akan bertemu pada jarak SA = 3tA2 = 48 m (dari titik P).
3. Grafik di bawah menghubungkan kocepatan V dan waktu t dari dua mobil A dan B, pada lintasan dan arah sama. Jika tg a = 0.5 m/det, hitunglah:
a. Waktu yang dibutuhkan pada saat kecepatan kedua mobil sama.
b. Jarak yang ditempuh pada waktu menyusul
Jawab:
a. Percepatan kedua benda dapat dihitung dari gradien garisnya,
jadi : aA = tg a = 0.5
10/t = 0.5 ® t = 20 det
aB = tg b = 40/20 = 2 m/det
b. Jarak yang ditempuh benda
SA = V0 t + 1/2 at2 = 30t + 1/4t2
SB = V0 t + 1/2 at2 = 0 + t2
pada saat menyusul/bertemu : SA = SB ® 30t + 1/4 t2 = t2 ® t = 40 det
Jadi jarak yang ditempuh pada saat menyusul : SA = SB = 1/2 . 2 . 402 = 1600 meter
5. Gerak Berbentuk Parabola
Gerak ini terdiri dari dua jenis, yaitu:
1. Gerak Setengah Parabola
Benda yang dilempar mendatar dari suatu ketinggian tertentu dianggap tersusun atas dua macam gerak, yaitu :
| a. | Gerak pada arah sumbu X (GLB) vx = v0 Sx = X = vx t | |
| b. | Gerak pada arah sumbu Y (GJB/GLBB) vy = 0 ]® Jatuh bebas y = 1/2 g t2 |
Benda yang dilempar ke atas dengan sudut tertentu, juga tersusun atas dua macam gerak dimana lintasan
dan kecepatan benda harus diuraikan pada arah X dan Y.
| a. | Arah sb-X (GLB) v0x = v0 cos q (tetap) X = v0x t = v0 cos q.t | Gbr. Gerak Parabola/Peluru |
| b. | Arah sb-Y (GLBB)v0y = v0 sin q Y = voy t - 1/2 g t2 = v0 sin q . t - 1/2 g t2 vy = v0 sin q - g t |
top = v0 sin q / g
sehingga
top = tpqtoq = 2 top
OQ = v0x tQ = V02 sin 2q / g
h max = v oy tp - 1/2 gtp2 = V02 sin2 q / 2g
vt = Ö (vx)2 + (vy)2
Contoh:
1. Sebuah benda dijatuhkan dari pesawat terbang yang sedang melaju horisontal 720 km/jam dari ketinggian 490 meter. Hitunglah jarak jatuhnya benda pada arah horisontal ! (g = 9.8 m/det2). Jawab:
| vx = 720 km/jam = 200 m/det. h = 1/2 gt2 ® 490 = 1/2 . 9.8 . t2 t = 100 = 10 detik X = vx . t = 200.10 = 2000 meter |
Jawab:
Peluru A:
hA = V02 sin2 30o / 2g = V02 1/4 /2g = V02 / 8g
Peluru B:
hB = V02 sin2 60o / 2g = V02 3/4 /2g = 3 V02 / 8g
hA = hB = V02/8g : 3 V02 / 8g = 1 : 3
6. Gerak Melingkar
Gerak melingkar terbagi dua, yaitu:
1. GERAK MELINGKAR BERATURAN (GMB)
GMB adalah gerak melingkar dengan kecepatan sudut (w) tetap.
| Arah kecepatan linier v selalu menyinggung lintasan, jadi sama dengan arah kecepatan tangensial sedanghan besar kecepatan v selalu tetap (karena w tetap). Akibatnya ada percepatan radial ar yang besarnya tetap tetapi arahnya berubah-ubah. ar disebut juga percepatan sentripetal/sentrifugal yang selalu | v.
v = 2pR/T = w R
ar = v2/R = w2 R
s = q R
|
GMBB adalah gerak melingkar dengan percepatan sudut a tetap.
Dalam gerak ini terdapat percepatan tangensial aT = percepatan linier, merupakan percepatan yang arahnya menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan v).
a = Dw/Dt = aT / R
aT = dv/dt = a R
T = perioda (detik)
R = jarijari lingkaran.
a = percepatan angular/sudut (rad/det2)
aT = percepatan tangensial (m/det2)
w = kecepatan angular/sudut (rad/det)
q = besar sudut (radian)
S = panjang busur
Hubungan besaran linier dengan besaran angular:
| vt = v0 + a t wt S = v0 t + 1/2 a t2 | Þ w0 + a t Þ q = w0 + 1/2 a t2 |
1. Sebuah mobil bergerak pada jalan yang melengkung dengan jari-jari 50 m. Persamaan gerak mobil untuk S dalam meter dan t dalam detik ialah:
S = 10+ 10t - 1/2 t2
Hitunglah:
Kecepatan mobil, percepatan sentripetal dan percepatan tangensial pada saat t = 5 detik !Jawab:
v = dS/dt = 10 - t; pada t = 5 detik, v5 = (10 - 5) = 5 m/det.
- percepatan sentripetal : aR = v52/R = 52/50 = 25/50 = 1/2 m/det2
- percepatan tangensial : aT = dv/dt = -1 m/det
Tahap penguasaan mahasiswa dievaluasi selain dengan UTS dan UAS juga melalui pekerjaan rumah (PR).
Buku sumber utama:
Halliday & Resnick.
(1989).FISIKA; Tipler. (2001).FISIKA Untuk Sains dan Teknik.
Selamat
Belajar







Tidak ada komentar:
Posting Komentar